Défi mathématique : Dévoilez la solution à ce casse-tête énigmatique

Une énigme mathématique intrigante suscite des débats enflammés en ligne, défiant à la fois les écoliers et les parents à résoudre un problème en apparence simple. Découvrez pourquoi cette équation basique peut semer la confusion et stimuler l'esprit critique.
Le défi revisité
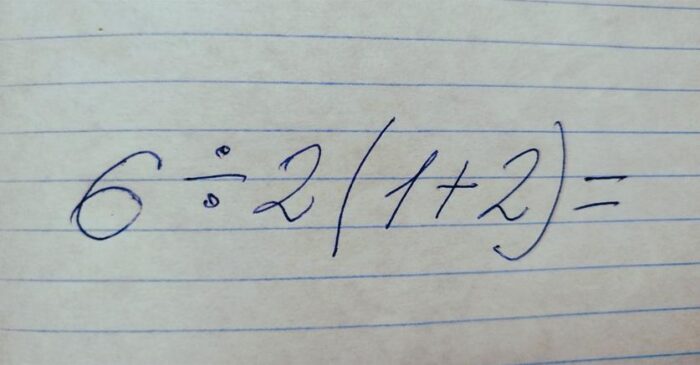
L’équation mystère à résoudre est : 6 ÷ 2(1 + 2) = ?
Un défi logique et mathématique
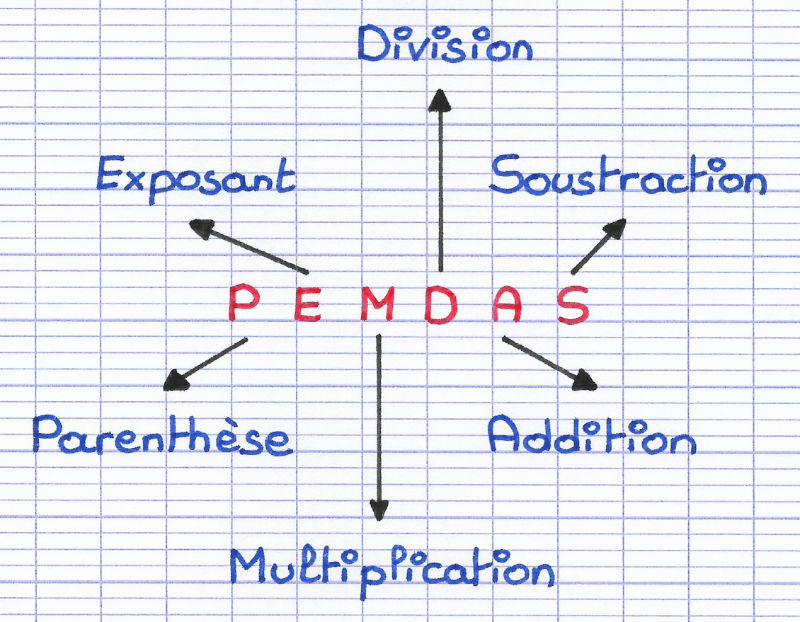
Au premier abord, certains pourraient être tentés de multiplier avant de diviser, mais il est crucial de respecter les règles de priorité des opérations connues sous l’acronyme PEMDAS (Parenthèses, Exposants, Multiplication et Division, Addition et Soustraction).
Analysons ceci pas à pas :
-
Résolution des parenthèses en premier
1 + 2 équivaut à 3
L’équation se transforme alors en :
6 ÷ 2(3)
-
Division avant multiplication
Contrairement à ce que l’on pourrait penser, la multiplication et la division ont la même priorité et doivent être traitées de gauche à droite.
Ainsi, nous divisons d’abord :
6 ÷ 2 égale 3
Puis nous multiplions :
3 × 3 donne 9
La solution finale :

La réponse correcte est donc 9, et si vous l’avez résolue, félicitations !
Pourquoi tant de perplexité ?
La confusion provient principalement de la manière dont l’équation est formulée. Beaucoup interprètent le « 2(3) » comme une multiplication implicite à résoudre avant la division, pensant qu’il s’agit d’une forme factorisée. Néanmoins, selon les conventions mathématiques, la division et la multiplication doivent être abordées dans l’ordre de lecture, de gauche à droite.
L’importance de la cohérence en mathématiques
Ces malentendus soulignent l’importance d’enseigner aux jeunes (et aux adultes !) les bonnes méthodes de résolution. Les mathématiques reposent sur des règles précises qui, lorsqu’elles sont appliquées correctement, conduisent toujours au bon résultat.
En conclusion
Si vous avez été perplexe, ne vous inquiétez pas, vous n’êtes pas seul ! Cette équation démontre que même les problèmes en apparence simples peuvent renfermer des nuances significatives. Ainsi, la prochaine fois que vous aiderez votre enfant avec ses devoirs, gardez en tête les règles de priorité et suivez-les méthodiquement pour éviter toute ambiguïté.