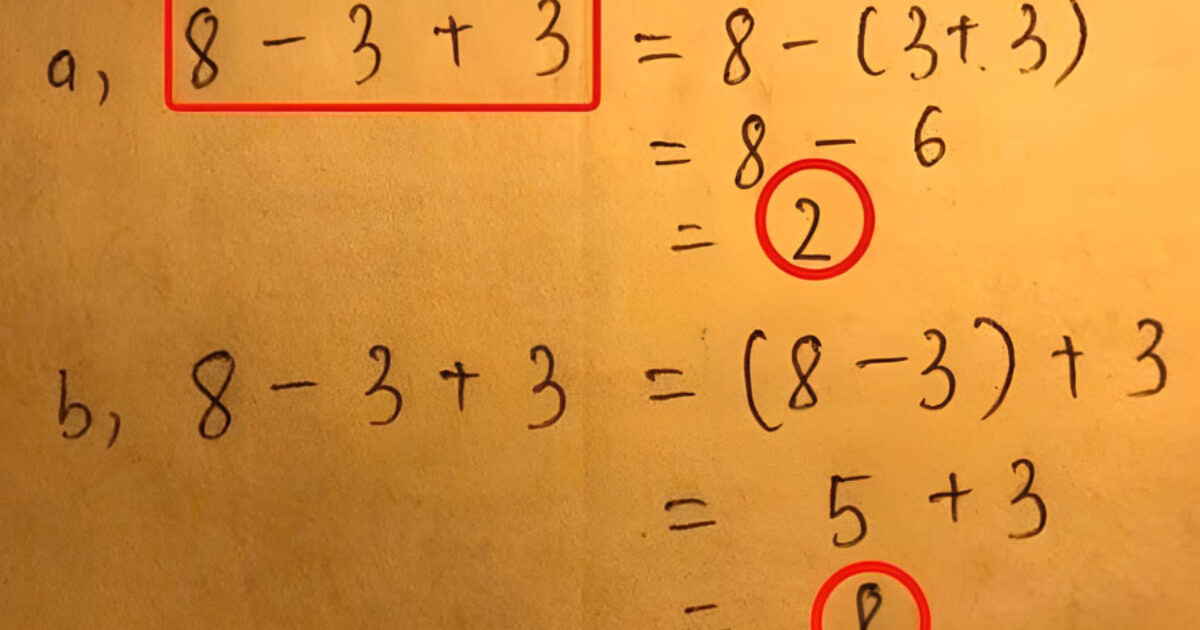Défi mathématique à résoudre : Testez vos compétences en calcul !

Découvrez les subtilités cachées derrière un problème mathématique en apparence simple. Mettez à l'épreuve votre maîtrise des opérations prioritaires dans ce défi captivant.
La confusion des priorités : pourquoi tant de personnes commettent des erreurs ?
Combien de fois avons-nous observé des situations simples créer de la confusion, même parmi les amateurs de mathématiques ? Prenons un exemple concret : 48 ÷ 8(14 – 8). Souvent, les règles de priorité des opérations sont mal interprétées. Pourquoi ? Parce que la multiplication implicite, symbolisée par la juxtaposition (comme dans 8(6)), n’est pas toujours évidente.
Voici ce qu’il est important de retenir :
- Les parenthèses englobent plus que leur contenu : elles incluent également tout facteur directement adjacent.
- La multiplication par juxtaposition a une priorité plus élevée que la division classique.
L’approche détaillée : la méthode correcte
Pour résoudre de manière précise l’équation 48 ÷ 8(14 – 8), il est essentiel de respecter l’ordre des opérations (PEMDAS ou BODMAS). Voici les étapes à suivre :
-
Résoudre ce qui se trouve à l’intérieur des parenthèses :
14 − 8 = 6.
Ainsi, l’équation devient : 48 ÷ 8(6).
-
Traiter la multiplication implicite :
En l’occurrence, 8(6) équivaut à 8 × 6 = 48.
Par conséquent, l’équation se transforme en : 48 ÷ 48.
-
Effectuer la division :
48 ÷ 48 = 1.
Résultat final : 1.
Pourquoi l’autre méthode est-elle erronée ?
De nombreuses personnes interprètent l’équation de la manière suivante :
-
Résolution des parenthèses :
14 − 8 = 6, ce qui conduit à 48 ÷ 8 × 6.
-
Division et multiplication de gauche à droite :
48 ÷ 8 = 6, suivi de 6 × 6 = 36.
Cette approche semble correcte mais néglige un point crucial :
La multiplication par juxtaposition (8(6)) a la priorité. Ignorer cela revient à enfreindre les règles de priorité des opérations.
Se souvenir des points essentiels : éviter les erreurs

Lorsque vous rencontrez un nombre accolé à des parenthèses (par exemple 8(6)), considérez cela comme une entité unique.
Toujours respecter l’ordre de priorité : Parenthèses > Multiplication implicite > Division.
En conclusion, ce défi va au-delà d’un simple exercice mathématique. Il met en lumière l’importance de saisir les subtilités des mathématiques pour éviter les erreurs face à des équations en apparence simples.