Cette illusion géométrique va vous faire douter de vos yeux
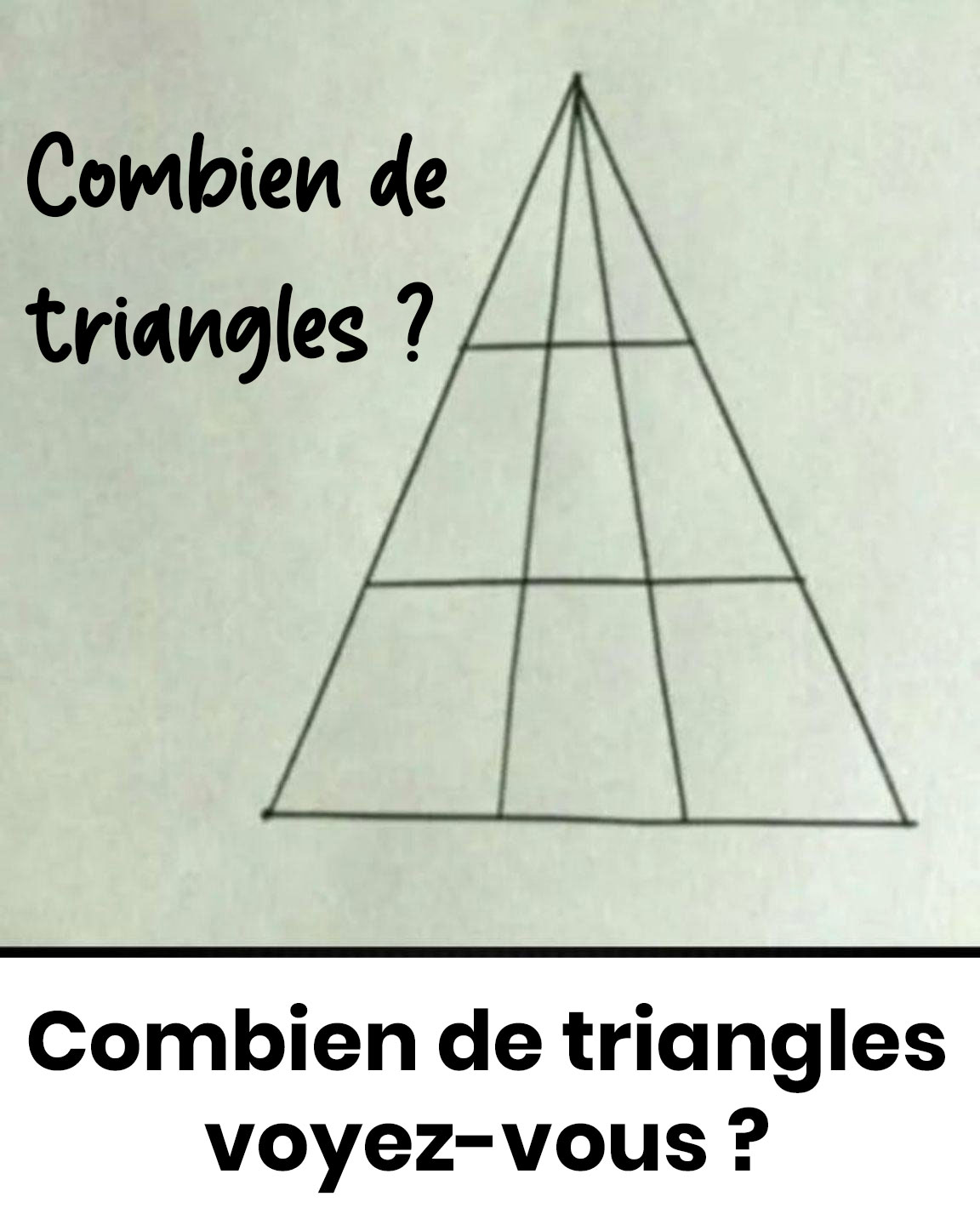
Ce casse-tête visuel en apparence simple résiste farouchement à notre intuition. Derrière sa structure triangulaire élémentaire se dissimulent bien plus de formes que notre cerveau ne veut bien l'admettre. Préparez-vous à découvrir la méthode infaillible pour percer son secret et épater votre entourage.
Le défi des formes insaisissables
Notre perception a tendance à capturer les triangles les plus manifestes, en négligeant ceux qui émergent de l’assemblage de plusieurs sections. Conséquence : nous tombons généralement en dessous du compte réel. Dans cette disposition classique où quatre niveaux sont créés par trois traits parallèles au côté inférieur, la solution exacte s’élève à 27.
Si votre estimation personnelle avoisinait les 26 unités, vous avez vraisemblablement manqué l’un des grands triangles composites – généralement celui qui s’élève sur trois étages ou une version plus modeste sur un côté.
La technique systématique pour un décompte précis

Concentrez-vous d’abord sur les triangles orientés vers le sommet, classés par échelle :
- Échelle minimale (1 niveau) : 10 occurrences
- Échelle moyenne (2 niveaux) : 6 occurrences
- Échelle large (3 niveaux) : 3 occurrences
- Échelle maximale (4 niveaux) : 1 occurrence
Addition partielle pour l’orientation supérieure : 10 + 6 + 3 + 1 = 20.
Incorporez ensuite les triangles inversés générés par l’entrelacement des segments : 7 unités.
Résultat définitif : 20 + 7 = 27.
Pour mémoriser facilement : retenez « 20 pour les pointes vers le ciel, 7 pour celles tournées vers la terre » et vous échapperez à l’erreur commune.
L’élégance mathématique derrière le puzzle

Vous préférez une approche plus théorique ? Lorsqu’un triangle principal est segmenté en n rangées via des lignes parallèles à sa base (dans notre cas n = 4), cette équation donne la réponse :
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Avec n = 4 :
T = 4 × 6 × 9 ÷ 8 = 27
Ce chiffre concorde parfaitement avec notre inventaire méticuleux. La force de cette formulation réside dans sa capacité à englober toutes les configurations imaginables, même les plus complexes. Parfait pour confirmer son intuition… ou remporter une discussion animée entre amis !
Pièges récurrents (et comment les contourner)
- Décompter « par étages » sans considérer les formes traversant plusieurs niveaux : le principal fautif étant souvent le triangle s’étendant sur trois hauteurs.
- Négliger les triangles inversés : moins saillants visuellement, ils comptent pourtant pour 7 unités précieuses.
- Imaginer des lignes verticales supplémentaires : certaines versions du défi intègrent effectivement des verticales, ce qui influence le total (mais jamais vers 26). Vérifiez toujours la configuration exacte avant de statuer.
- Compter deux fois certaines formes : adoptez une progression méthodique par taille pour prévenir les répétitions.
Pour approfondir le challenge
- Modifiez le nombre de divisions : expérimentez la formule avec n = 3 ou n = 5 et confrontez avec un décompte visuel – excellent pour aiguiser votre regard.
- Jouez contre la montre : accordez-vous 60 secondes pour arriver à 27. La clé ? Identifiez d’abord les triangles ascendants, puis ajoutez leurs homologues descendants.
- Transmettez la méthode : partager une technique, c’est l’ancrer durablement dans sa mémoire (et s’assurer de briller lors des prochains défis collectifs).
Car derrière une forme géométrique apparemment basique se niche souvent une leçon de logique implacable… et la satisfaction délicieuse de posséder la solution ultime !